Master the Fourier Transform
with this Visual, Intuitive, and Comprehensive Book Series

Calling all engineers!
Are you struggling to wrap your head around the mathematics of the Fourier Transform? This two-book series is specifically designed to demystify this challenging subject and help you conquer the math with ease.
What is the Fourier Transform?
What sets this series of books apart?
Visual and Intuitive Approach:
Gone are the days of drowning in complex equations and abstract explanations. These books leverage the power of visuals, diagrams, and graphs to present the Fourier Transform in a way that resonates with your engineering mindset.
Clear Explanations:
Understanding the math is crucial, and I aim to make it accessible to those who find all equations just an incomprehensible load of Greek letters. I break down the concepts into bite-sized, digestible pieces, guiding you through each step of the transformation process.
Numerical Work-Throughs:
Step-by-step numerical work-throughs clearly guide you through actually calculating the Discrete and Fast Fourier Transforms for a real signal.
Links to Interactive Demos & Animations:
Discover the fundamental ideas behind the Fourier Transform by playing with interactive demonstrations and animations. These tools let you see how altering the equations immediately affects the outcome.
What will you learn?

Who was Fourier?
A look at the man behind the math. Did you know that not only was Fourier a mathematical genius but a political activist, an Egyptologist, and one of Napoleon's scientific advisors? How did Fourier arrive at his groundbreaking idea?
Sine Waves
What are the properties of a sine wave? How can we combine sine waves with different properties to produce more complex signals?
Complex Numbers
What are complex numbers and how do we use the language of complex numbers to perform the mathematical operations required to calculate the frequency spectrum of a signal?
Convolution
How does sliding one signal over another help us locate and identify the different sinusoids within a signal? What was the shortcut that Fourier used to find them quicker?

From Series to Transform
How did the Fourier series become the Fourier transform? What was the problem with the Fourier Series that necessitated this development?
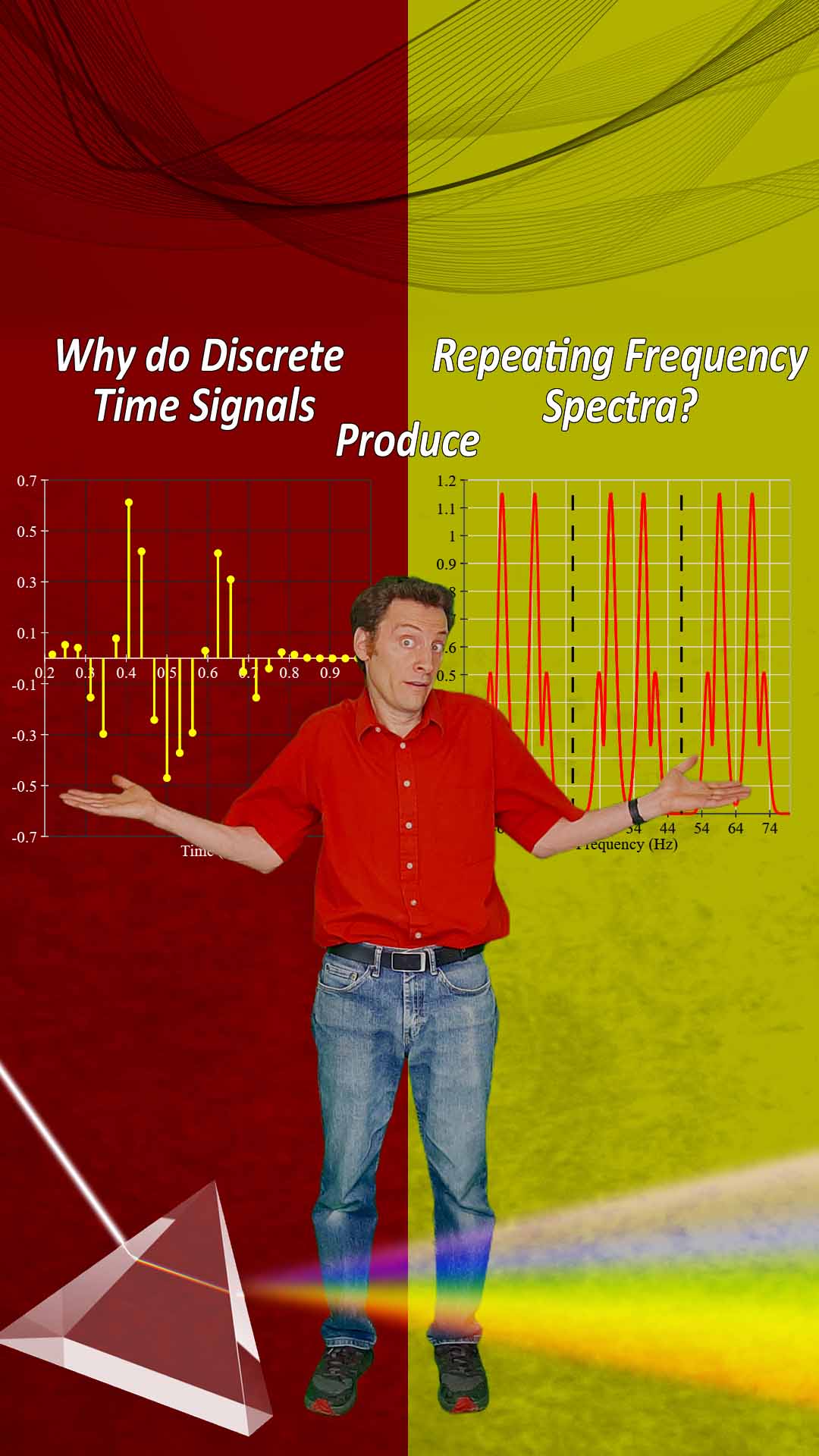
The DTFT
With the advent of the digital age, the number of practical applications for Fourier’s theories exploded. As the Fourier Transform took its first steps into the digital age, we look at how it dealt with discrete-time signals.
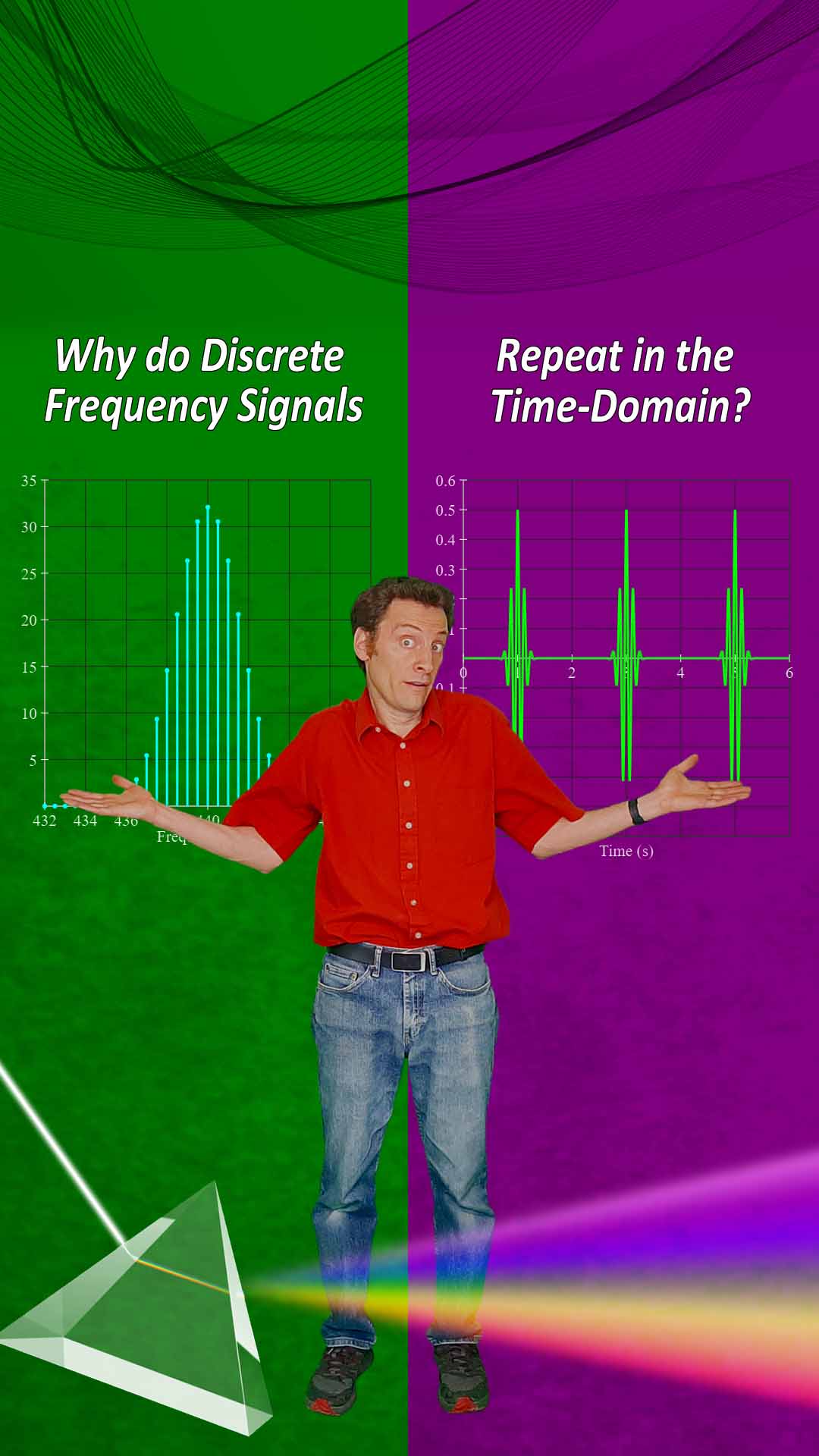
The DFT
Time isn’t the only thing that can be discrete. Frequency can also be discrete. The DFT was a major development of Fourier’s theories that helped turn the Fourier Transform into something that could be applied to almost any real-world signal.
Windowing Functions
What happens when your signal is longer than the number of samples you can fit in your DFT? You have to split it up into frames. However, this causes spectral leakage. What is spectral leakage and how do Windowing Functions reduce the problem?
How the FFT works
A detailed, intuitive, and visual look into how the FFT saves so much computing power by efficiently arranging the calculations into simple, repeatable blocks, turning the DFT into something most modern-day CPUs can handle with ease.
About the Author

Mark Newman is an Electronics Engineer with over 25 years of professional experience. He is a graduate of the Manchester University School of Electrical and Electronic Engineering in the UK. He has developed products ranging from robots for milking to devices for feeding and monitoring patients in intensive care, spending many hours analysing signals and implementing mathematical models. Today he manages a successful YouTube channel, producing educational videos for electronics students studying signals and systems. His emphasis on intuitive learning and visually demonstrating what the equations mean, has helped thousands of students to properly understand the mathematical principles they need to succeed.
Request a sample
Would you like to receive sample chapters from each of the books? Fill out the form below and they will be sent to your email in PDF format.
What do people say?


More on the Fourier Transform
Click on a thumbnail in the carousel below to open the selected video.



















Frequently Asked Questions
-
Who are these books for?
These books are suitable for anyone curious about the Fourier Transform, whether you're a student, an engineer, a scientist, or simply someone interested in gaining a deeper understanding of this fundamental mathematical concept. They're designed to be accessible to both beginners and those with some prior knowledge of the topic.
-
Are these books suitable for self-study?
Yes, absolutely! They have been specifically designed to be a self-study-friendly resource. The books are structured with clear explanations and examples, making them accessible for independent learners.
-
Are there supplementary materials included with these books?
Yes, the books include links to videos, interactive demonstrations, and animations all designed to help enrich your learning experience.
-
Can I read one book without the other?
The books are very much intended as a series. The assumption is that someone reading "How the Fourier Transform Works" has either already read, or already knows the concepts covered in "How the Fourier Series Works".
"How the Fourier Series Works" looks at Fourier's original theory and covers the fundamental principles used in both the Fourier Series and the Fourier Transform.
"How the Fourier Transform Works" builds on the knowledge gained in the first book. We look at the developments made to the Fourier Series by Dirichlet and others, initially turning it into the Fourier Transform and then the Discrete and Fast Fourier Transforms which are in use so widely today. The first book covers a number of concepts that are used in the second book, but not explained in as much detail. -
How can I purchase the books?
The books are available from Amazon.com or your local Amazon store in both Kindle eBook and paperback formats. Simply click on the "Shop Now" button at the bottom of the page to order your copies.
-
What if I have questions or need further assistance?
I will do my best to help you! If you have any questions or need assistance, please write to me at [email protected]
-
Is there a money-back guarantee?
Yes! If you're not completely satisfied with these books, please refer to the Amazon.com Returns Policy for details on how to request a refund.