Master the Fourier Transform visually and intuitively
An Online Course for Students and Engineers
Buy Now
We all learn in different ways, but the classic way of teaching scientific concepts is through blackboards filled with incomprehensible mathematical formulae. How the Fourier Transform Works is the first of 2 online courses with a difference. It uses the power of video and animation to try and demystify the maths behind one of the cornerstones of signal analysis and explain how it works in a clear, visual, and intuitive way.
The second course: “The Fourier Transform: From Theory to Practice” (currently in development) will address turning the theory of the Fourier Transform into the practical tools we have today like the DFT and FFT.
“Most of the fundamental ideas of science are essentially simple, and may, as a rule, be expressed in a language comprehensible to everyone.” – Albert Einstein
The video below introduces the courses and thier aims.
Latest Updates |
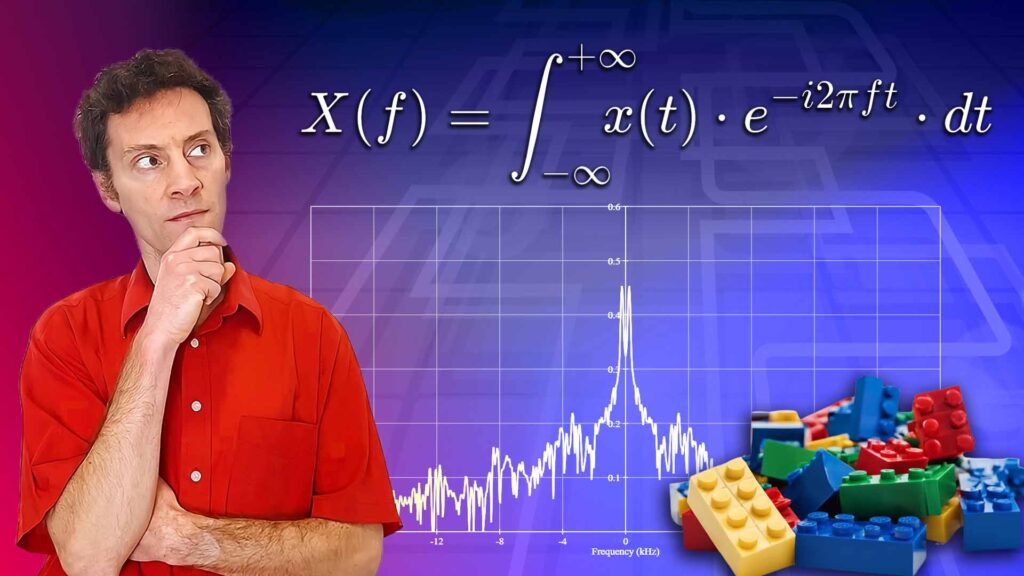
How the Fourier Transform Works
I am excited to announce the publication of my new book: How the Fourier Transform Works, completing the journey we began in my last book: How the Fourier Series Works.
In the book, we find out how the Fourier Transform models non-repeating signals and continue the journey right up to the present day through the DTFT and DFT, culminating in a detailed study of how the FFT works.
Modern Digital Filter Design | Advice from an expert
Modern digital filter design is key to extracting the data we need from our noisy world. But where do we start? What must we take into account before beginning to design a digital filter? What tools are there out there to help us?
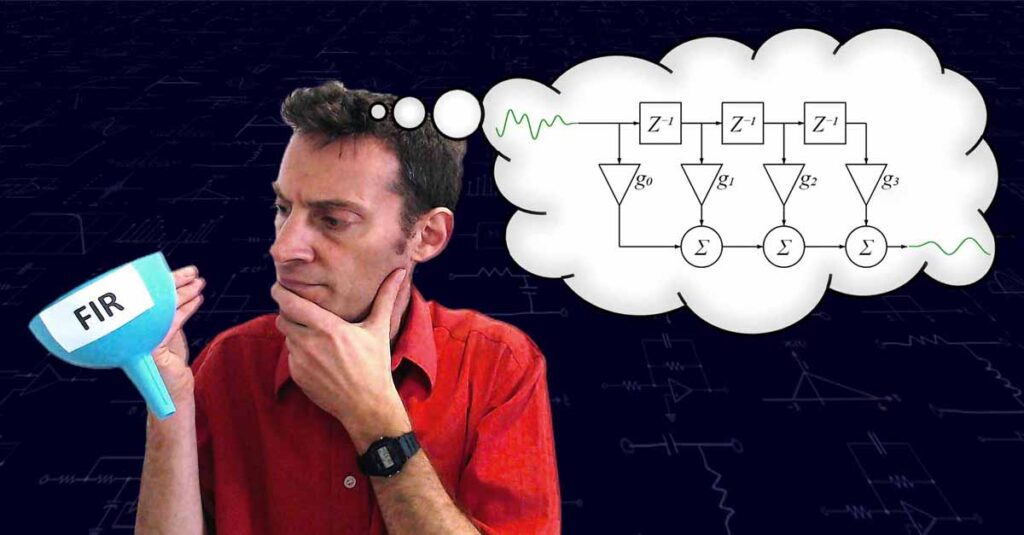
How FIR filters work | Applying the filter
In this post, we discover how to use a filter’s impulse response to filter a signal. Included in the post are snippets of JavaScript code demonstrating how you can write your own FIR filter.
How FIR filters work | Making a practical filter
Filters are practical things. Therefore they need to work in the real world. How can we turn a mathematical equation into something that actually works?
How FIR filters work | Designing the filter
How to use the inverse Fourier Transform to tailor the impulse response of our filter to give us the frequency response we are looking for.
How FIR filters work | Introduction
How do FIR filters work? If you’ve ever calculated a running average, then you have a partial answer to this question. We look how a running average is a sort of convolution, and convolution is how FIR filters work.
Negative Frequency, Imaginary Numbers, and the Complex Conjugate
What is negative frequency? Why do we need it? What have imaginary numbers got to do with it? Is it a physical phenomenon or just a quirk of the maths? In this video, we look at what makes a signal real and why negative frequencies make them so.
Understand the output of the FFT | Magnitude and Phase
The output of the FFT is just a list of complex numbers. But, we are used to seeing the FFT of a signal represented as a graph of magnitude or phase plotted against frequency. In this video, I explain how to convert the output of the FFT into the magnitude and phase graphs we know and love.
How the Fourier Series Works
I’m really proud and excited to be publishing my first book called “How the Fourier Series Works.” The book is aimed at students, guiding them systematically through each of the core concepts making up the Fourier Series. By taking a visual approach, the book grants students an intuitive understanding of Fourier’s ideas, providing them with the basis they need to confidently use one of the cornerstones of signal analysis.
Understand the output of the FFT | Frequency
The output of the FFT can be quite confusing. All you are presented with is a list of complex numbers that, at first glance, don’t tell you anything about the frequencies present in your signal. In this video, we find out how to find the frequency information in the output of the FFT.
The imaginary number i and the Fourier Transform
i and the Fourier Transform; what do they have to do with each other? The answer is the complex exponential. It’s called complex because the “i” turns an exponential function into a spiral containing within it a cosine wave and a sine wave.
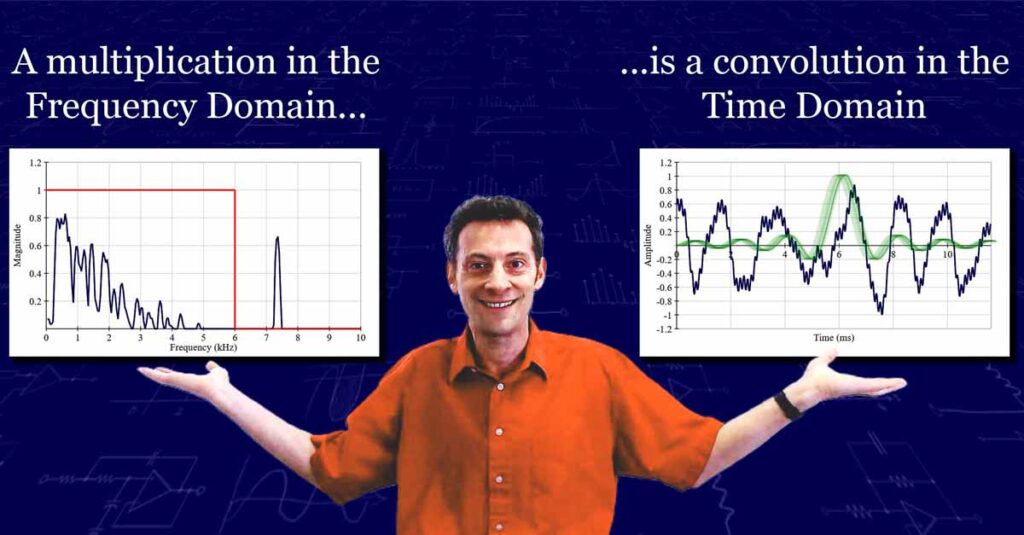
Convolution and the Fourier Transform
The Fourier Transform uses convolution to convert a signal from the time domain into the frequency domain. In this video I demonstrate an intuitive way of understanding what convolution is, explain the convolution equation and demonstrate how it is used in the Fourier Transform.